HUP – What is h-bar?

The Heisenberg Uncertainty Principle (or HUP – homemade abbreviation) is one important quality of Quantum Mechanics. It goes like this:

It is impossible to specify simultaneously, with arbitrary precision, both the momentum and the position of a particle

In a more blunt manner: If I know very well the position of a particle, I know its momentum rather loosely. And viceversa. I know very well the momentum, don’t know much about the position.

This is very strange from our daily life standpoint. We have no problems to measure both the position and the momentum (or velocity) of the stuff around us.

The mathematical expression for the HUP (one of them, at least) is:

The σ are the respective standard deviations of x and p, they simply indicate how well we know our values. Let’s call it uncertainty. Example: the smaller σ_x is, the better we know x.

 is just a constant number. It is the Planck’s constant, and it is characteristic of Quantum Physics. Indeed, you’ll find it constantly and almost everywhere, somewhere in the formulae, if you study Quantum Mechanics.

Here I want to give a flavor of how  can be interpreted. It can be thought as a measure of the scale at which quantum effects are relevant and appreciable.

First, its value is very small.

Recall the equation I gave for the HUP:  

 

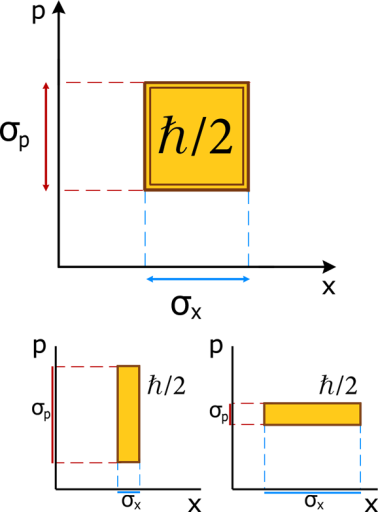
Let’s consider just the case where: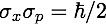 

Next I just represent this relation graphically, so that it’s easy to see what it implies:

The point is, the value of the area in yellow remains constant. We can play around with the values of σ_x and σ_p separately. But alas if we make one small the other will necessarily become larger, because they have to preserve the area. So, again, the HUP represents a constraint in the accuracies of both x and p simultaneously.

Now, if  is that small, this area which cannot be made smaller is already really very small. That is why the HUP is hidden to us, since the scales of size and momentum in our everyday life are far larger by many orders of magnitude. This tininess rendered quantum effects undetectable up to until the late XIX c.

As long as the size, the velocity, or the mass (remember that p = mv) of an object become large enough, quantum effects become negligible in comparison. Not because they are not there, but simply because they are so ridiculously small compared to the accuracies in position and momentum that we’d like to have, that we can totally ignore them.

By the way, a representation of position in one axis and momentum in the other is a representation of the phase space.

The inequality in  simply means that we may be as well less accurate.

Note that standard deviations are a statistical thing. To know it, we need to do measurements over a bunch of particles, not just one.

IMPORTANT: This is a physical limit for accuracy! It’s not the fault of our instruments! An alien culture 10,000 years more technologically advanced than us cannot go either beyond this accuracy. Or, if we could ask an electron, so to say, not even the electron itself would know both its position and momentum more precisely.